一万多年以前,当伊比利亚半岛上的洞穴人首次从蜂蜜中提取出粘长的细丝时,人类便开始了对液桥拉伸的思考。时至今日,液桥拉伸已经在诸如打印、聚合物生产等方面取得了广泛的应用,但是其部分物理机制仍然是未解之谜。

近日,浙江大学机械工程学院邹俊课题组在该方向取得重要进展,论文Statics and dynamics of a viscous ligament drawn out of a pure-liquid bath发表于国际流体力学顶级期刊Journal of Fluid Mechanics。该论文为邹俊课题组与比利时布鲁塞尔自由大学Scheid Benoit教授课题组合作成果,论文第一作者为博士生魏啸峰,通讯作者为邹俊教授和Benoit Scheid教授。

https://doi.org/10.1017/jfm.2021.505
基本原理
想象我们用筷子从蜜池中提拉出一根细长的蜂蜜液桥,随着筷子向上运动,我们将观察到液桥逐渐演变成一根绵长的细丝并最终断裂。在这个典型现象中,主要有两个物理效应:延性效应和毛细效应。所谓延性效应是指液桥单纯由于拉伸引起的收缩,是蜂蜜能被拉伸成细丝的原因。而毛细效应是指液桥由于表面张力的存在而造成的扰动自增效应,一般也称为Rayleigh-Plateau不稳定原理,它导致了蜂蜜的最终断裂。
然而由于液桥拉伸具有强烈的瞬态效应,这两个效应在拉伸中具体起到的作用一直没有得到系统的研究。我们在这篇论文中对问题进行了系统的数值模拟,并定量分析了其中的物理机理。
问题的描述
物理场景:在无限大液池中,从静态弯液面出发对液桥进行拉伸直至断裂。主要关注轮廓发展以及最终的断裂高度。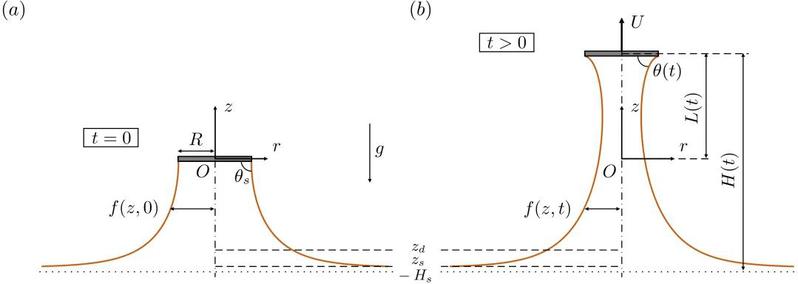
我们采用1993年Eggers提出的一维模型对问题进行研究,主要的动量方程为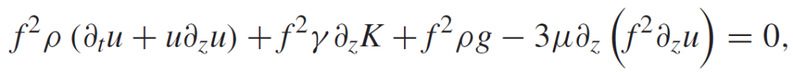
数值模拟结果
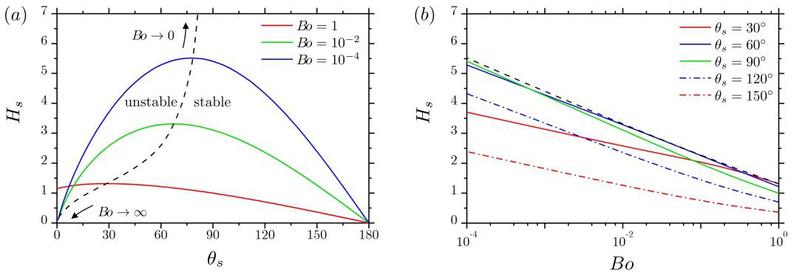
静态液桥高度可以表达为弯液面角(a)和杆件半径(b)的函数。结果如图所示:(a)静态液桥可以分为稳定区间和不稳定区间;(b)我们独立发现了液桥高度解析式。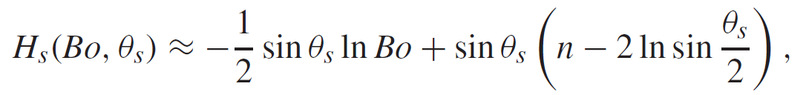
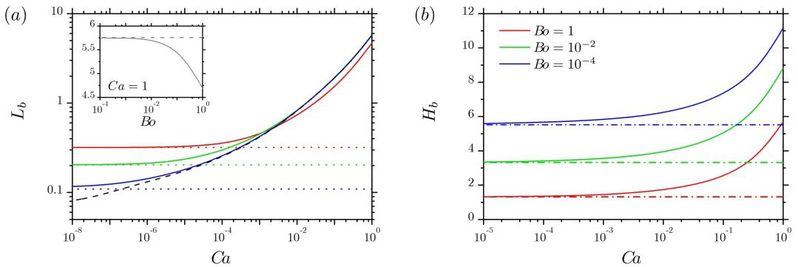
在静态拉伸的基础上我们进行动态拉伸计算,结果如上图所示。断裂高度可以表达为
右侧两项分别代表初始静态高度和动态断裂长度。断裂长度存在无重力极限和静态极限,且具有一无重力拉伸区间,其拉伸相图如下。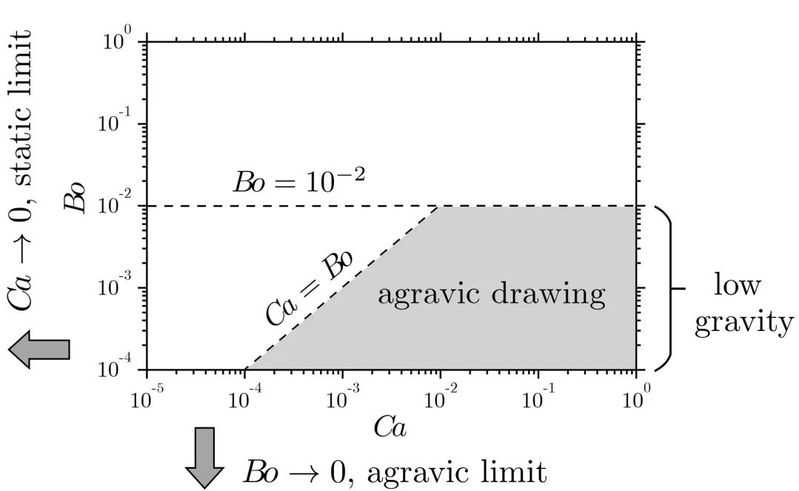
机理分析
一个典型的拉伸过程如图所示,(a)线性坐标轮廓,(b)对数坐标轮廓,(c)轴向速度。

以(b)中的虚线为界,拉伸过程可以分为延性阶段和毛细阶段:在延性阶段中,液桥以相似的模式发展;在毛细阶段中,液桥在表面张力作用下快速收缩断裂。借助延性阶段的近似解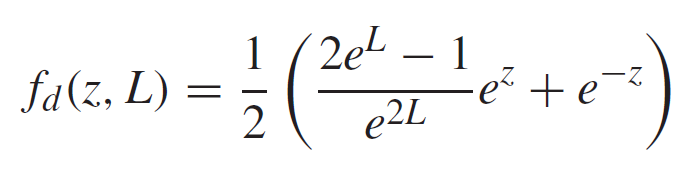
我们可以将延性、毛细效应解耦:无论液桥以何种速度拉伸,其初始阶段均满足一系列与拉伸速度无关的空间函数(轮廓),每一个轮廓均对应于一簇延性收缩速度和一个毛细收缩速度。数值结果表明,我们的理论(方块)很好的预测了两个阶段之间的过渡。

实验验证
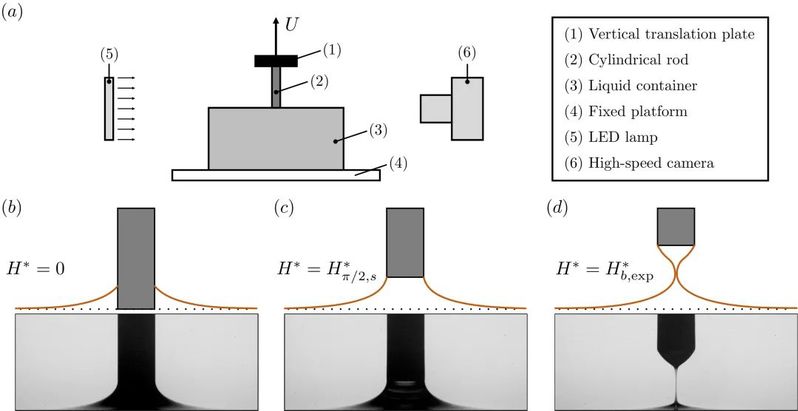
我们采用实验对数值模拟结果进行验证,方案如上图所示。实验结果表明,整体而言数值模拟的结果与实验吻合良好,同时也存在一定偏差:当拉伸速度较小时,数值结果相较于实验值偏高,而当速度较大时则相反。
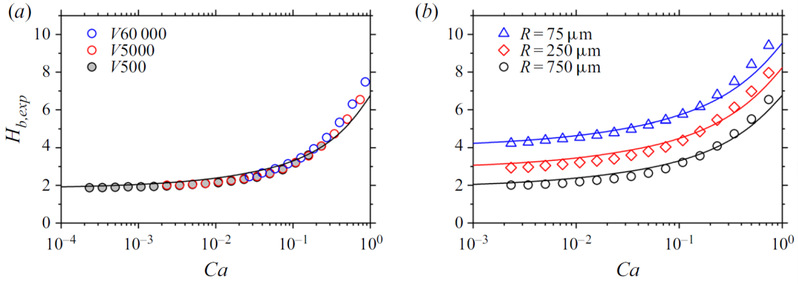
一维模型局限性
在比利时学者Javier的帮助下我们建立了二维模型并进行了对比分析。结果表明一维模型偏差是由于缺失了二维效应:内部的二维交互效应和底部的二维排水效应。应当指出,虽然具有一定局限性,但是一维模型能够以简洁、便捷的方式揭示液桥的物理机理,故而一直被广泛应用。
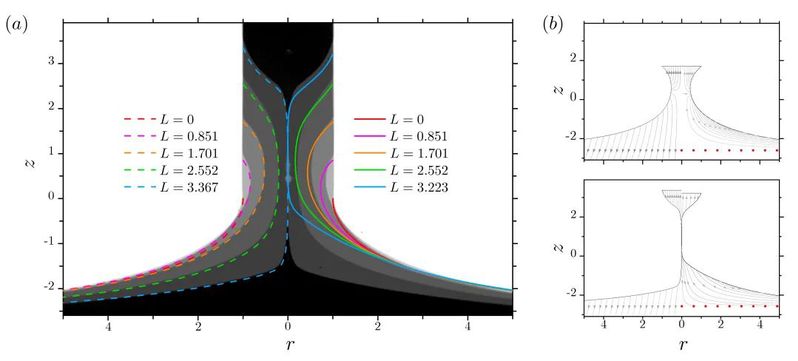
结论
我们采用一维模型,对从液池中拉伸出的液桥进行了静态和动态分析。着重分析了延性效应和毛细效应的相互作用关系。采用实验方法对数值结果进行了验证,并用二维模型对比分析了一维模型的局限性。
心路历程
◆ ◆ ◆
这篇论文从开始研究到最终录用经历了一年半时间,期间从独自出国、探索方法、经历疫情到回国成稿经历了诸多磨砺。回想起来,2019年深秋抵达布鲁塞尔机场时的忐忑不安至今记忆犹新。在比利时的半年我依次完成了建模、静态分析、动态分析。主要感想有几点:
1. 调研和交流很重要。这里十分感谢林方烨同学、Lionel博后和Julien博后在本研究中提供的帮助。
2. 科研需要静心探索。许多论文中一笔带过的内容,在实际研究中耗费了几周甚至更长的时间。例如静态数学原理是在反复尝试了一两周之后,偶然间在屏幕中看到对数坐标曲线才找到的突破口。
3. 灵感是不断思考的产物。在动态研究中,我在尝试数十次求解延性解析解后一度觉得要放弃。然而4月初的一个凌晨,我突然想到:为什么不先凑出一个近似解呢?那一刻头顶似乎都在冒金光,原来灵感是真的存在的!尤其是在之后一周内我证明出了真正的解析解是不存在的,那一刻的灵感就更加显得精彩绝伦。
最后,感谢邹俊教授和Benoit教授的悉心指导。希望在后面的科研生涯中能再接再厉,继续在科研的道路上奋勇前行。

